パーセプトロンアルゴリズム
4.1.7
naoya_t
2012.8.5 PRML復々習レーン
naoya_t
2012.8.5 PRML復々習レーン
スタンフォード大CS学部の
が立ち上げた、Stanford他17大学116講義(※2012/8/5現在)をオンラインで無料で提供するベンチャー企業。
現時点では提供されている講義はCSを中心とした科学系が大半だが、今後人文系の講義も増やしていくとのこと。
Machine Learning (Andrew Ng)
Probabilistic Graphical Models (Daphne Koller)
Natural Language Processing (Dan Jurafsky, Christopher Manning)
視覚と脳の機能をモデル化した線形分離アルゴリズム。
Frank Rosenblatt (1928-1969) が50年以上前 (1958) に提案。 ニューラルネットワーク研究の礎として、パターン認識アルゴリズムの歴史の中で重要な地位を占めてきた。
当初は電動可変抵抗や電気モーターを利用したアナログハードウェアとして実装され、簡単な形や文字を識別するための学習などに用いられた。
単純なパーセプトロンは線形分離不可能な問題を解けないが、多層化し誤差逆伝播を行うことで線形分離不可能な問題にも適用できるようになった。
入力データ 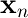 (に非線形変換
(に非線形変換
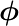 を適用した特徴量
を適用した特徴量
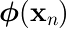 )に対し、
)に対し、
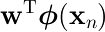 の値が
クラスC1なら正、C2 なら負になるように最適な重みベクトル
の値が
クラスC1なら正、C2 なら負になるように最適な重みベクトル
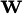 を学習する。
を学習する。
誤分類されるパターンが多ければ大きく、少なければ 0 に近づくような誤差関数を設定し、
確率的勾配降下法によって 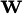 を求める。
を求める。
誤識別したパターンの総数を誤差関数とすれば自然だが、
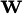 の変化に伴い変化する決定境界がデータ点を横切る度に不連続となるため
勾配がほとんどの場合 0 となってしまい、勾配降下法が効かない。
の変化に伴い変化する決定境界がデータ点を横切る度に不連続となるため
勾配がほとんどの場合 0 となってしまい、勾配降下法が効かない。
そこで別の誤差関数を考えたい。
目標変数 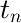 の値を { -1, +1 } とすれば、
の値を { -1, +1 } とすれば、
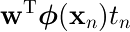 は
正しく分類される場合に正、誤分類なら負の値を取る。
は
正しく分類される場合に正、誤分類なら負の値を取る。
誤分類されたサンプル全てを含み、正しく分類されたサンプルは含まない集合
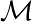 について
について
をパーセプトロン規準として定義する。
これを最小化する 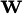 は確率的勾配降下法で求めることができる。
は確率的勾配降下法で求めることができる。
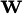 に定数を掛けても
に定数を掛けても
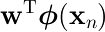 の正負は変化しないので、一般性を失うことなく
学習率パラメータ
の正負は変化しないので、一般性を失うことなく
学習率パラメータ 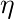 を 1 に設定することができる。
を 1 に設定することができる。
とかPRMLはしれっと言ってるんだけど、一般性を失うことなく云々って何? 学習率の設定によっては収束速度とか変わりそうなイメージがあるけどどうなの?
→sleepy_yoshiさんとのshuyoさんとの議論が参考になります:
結論から言うと
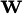 の初期値が 0 の場合は
の初期値が 0 の場合は 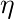 は収束速度に全く関係しない(同じ分離超平面に収束)
は収束速度に全く関係しない(同じ分離超平面に収束)3.1.3 (pp.141-142) 参照
個人的には大規模すぎるデータをシャッフルして(バッチではなく)1つずつ扱うのを「確率的 (stochastic) 勾配降下法」、次々現れるデータをオンライン的に扱うようなよくあるケースは「逐次的 (sequential) 勾配降下法」と呼ぶのがしっくりくる
あと勾配降下法 (gradient descent) / 最急降下法 (steepest descent) では個人的には勾配降下派だけれど
まあどっちでもいい
1回1回の更新には、誤分類されたパターンからの誤差への寄与を減少させる効果がある。
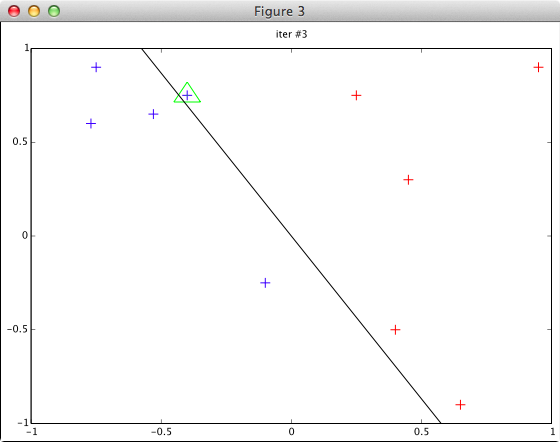
学習中の 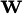 の変化によって、以前正しく分類されていたパターンを誤分類させるようなこともあり得る。
の変化によって、以前正しく分類されていたパターンを誤分類させるようなこともあり得る。
パーセプトロン学習規則は、各ステップで総誤差関数を減少させることを保証していない。
しかし、厳密解が存在する場合(=学習データ集合が線形分離可能な場合)には、このアルゴリズムは有限回の繰り返しで厳密解に収束することが保証される。
これがパーセプトロンの収束定理
とはいえ収束に必要な「有限回」はかなり多いので、実用的には分類不能なのか収束が遅いのか収束するまでわからない。
% データ読み込み
data = load('fig47dat.txt');
x = data(:, 1:2);
y = data(:, 3);
% w を適当に初期化
w = rand(1,2) * 0.001;
% η:学習率パラメータ
eta = 1;
% 確率的勾配降下法
maxiter = 100;
for t = 1:maxiter
plotData(x, y, w, t);
s = (x * w‘) .* y;
bad = find(s < 0);
if length(bad) == 0
break;
end
w += sum((x(bad,:) .* [y(bad) y(bad)]) * eta);
end
function plotData(x, y, w, t)
a = w(1,1); b = w(1,2);
figure(t); clf(); hold on;
title(sprintf('iter #%d', t));
axis([-1 1 -1 1]);
pos = find(y > 0); plot(x(pos,1), x(pos,2), '+b', 'markersize', 10);
neg = find(y < 0); plot(x(neg,1), x(neg,2), '+r', 'markersize', 10);
% 誤分類されたものに◯
s = (x * w‘) .* y;
bad = find(s < 0);
plot(x(bad,1), x(bad,2), 'og', 'markersize', 20);
% 決定境界に線を引く: ax + by = 0
if abs(a) <= abs(b)
plot([-1 1], [a/b -a/b], '-k', 'LineWidth', 1);
else
plot([b/a -b/a], [-1 1], '-k', 'LineWidth', 1);
end
hold off;
end
※データ (fig47dat.txt) は図4.7を見て適当に作成したもの
-0.75 0.9 1 -0.77 0.6 1 -0.53 0.65 1 -0.4 0.75 1 -0.1 -0.25 1 0.25 0.75 -1 0.4 -0.5 -1 0.45 0.3 -1 0.65 -0.9 -1 0.95 0.9 -1
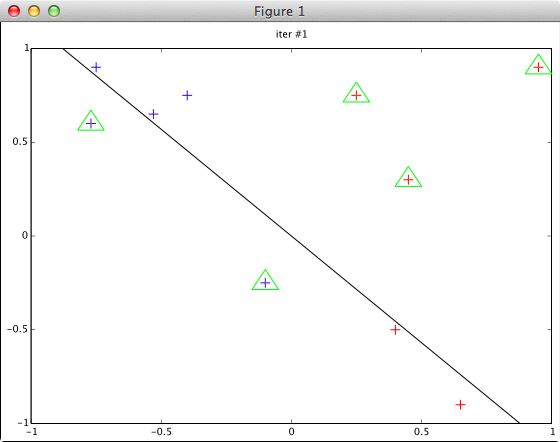
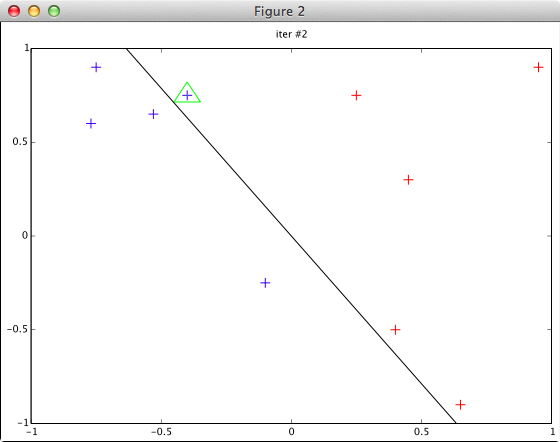
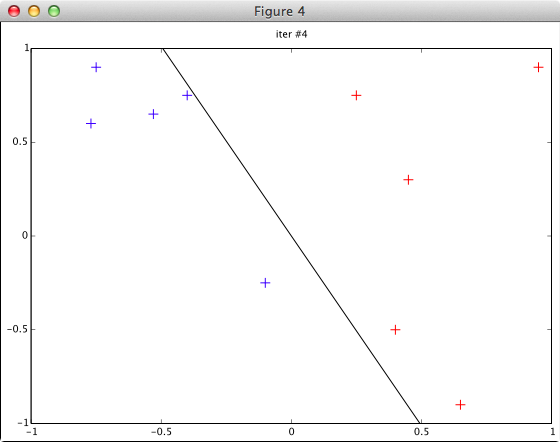
plotData() 関数に w = [0 0] 等を渡した場合のチェックを省いています。(完全なコードは発表資料と一緒に github に上げてあります)